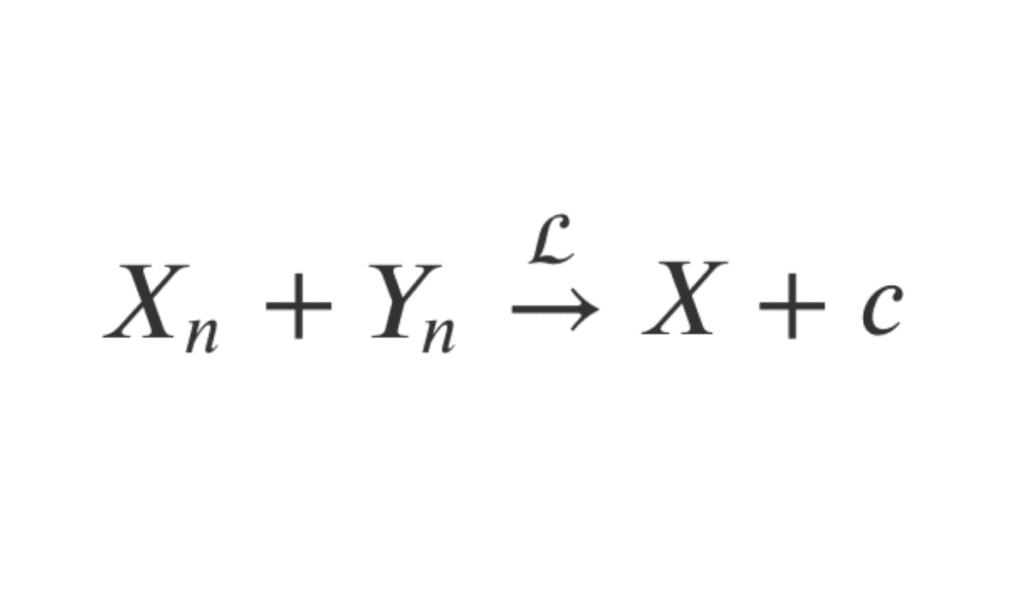Les notions hors programme se destinent surtout aux candidats visant les trois Parisiennes, mais cet article te propose de décortiquer le théorème de Slutsky, qui vient seulement d’être retiré du programme. Ce focus te permettra donc de mieux appréhender cette notion à l’aide d’exemples. Tu retrouveras aussi une liste de sujets d’annales qui l’utilisent pour pouvoir t’entraîner avant de rencontrer ce théorème en exercice !
Le théorème de Slutsky expliqué en français
Le théorème de Slutsky simplifie la recherche de la loi vers laquelle converge la somme et le produit de deux suites de variables aléatoires, que l’on nommera \(X_n\) et \(Y_n\), qui convergent l’une en loi vers \(X\), une variable aléatoire, et l’autre en probabilité vers une constante \(c\).
Ainsi, d’après le théorème de Slutsky, \(X_n+Y_n\) converge en loi vers \(X+c\) et \(X_nY_n\) converge en loi vers \(cX\).
Exemple concret
Prenons un exemple tiré du sujet de l’épreuve Maths II de 2011 (question 13b). On cherche la limite quand \(n\) tend vers \(+\infty\) de \(P([W_n \ge u_n])\), \(W_n\) étant une suite de variables aléatoires et \(u_n\) une suite réelle.
Grâce à la question précédente, on obtient que \(W_n\overset{\mathcal{L}}{\rightarrow}\frac{T}{2}\).
On sait également que \(\lim \limits_{n \to +\infty} u_n = -\frac{x}{\sqrt{2\pi}}\), \(x\) étant un réel. On peut alors considérer la suite \(u_n\) comme une suite de variables aléatoires et dire que \(u_n\overset{\mathbb{P}}{\rightarrow}-\frac{x}{\sqrt{2\pi}}\).
Ainsi, d’après le théorème de Slutsky, on sait que \(W_n-u_n\overset{\mathcal{L}}{\rightarrow}\frac{T}{2}+\frac{x}{\sqrt{2\pi}}\), et avec les autres éléments de l’exercice, on parvient à trouver la limite recherchée.
Définition mathématique du théorème de Slutsky
Soient \((X–n)\) et \((Y_n)\) des suites de variables aléatoires. Soit \(X\) une variable aléatoire et \(c\) une constante.
Théorème de Slutsky : Si \(X_n\) converge en loi vers \(X\), et si \(Y_n\) converge en probabilité vers une constante \(c\), alors le couple \((X_n,Y_n)\) converge en loi vers le couple \((X,c)\).
On peut alors écrire que si \(X_n\overset{\mathcal{L}}{\rightarrow}X\) et que \(Y_n\overset{\mathbb{P}}{\rightarrow}c\), alors on obtient que \(X_n+Y_n\overset{\mathcal{L}}{\rightarrow}X+c\) et que \(X_nY_n\overset{\mathcal{L}}{\rightarrow}cX\).
Quelques propriétés et rappels pour utiliser le théorème de Slutsky
Soient \((X–n)\) et \((Y_n)\) des suites de variables aléatoires dans \(\mathbb{R}\) et \(\mathbb{R}\). Soit \(X\) une variable aléatoire et \(c\) une constante.
- Si le couple \((X_n,Y_n)\) converge en loi vers le couple \((X,c)\), cela signifie en particulier que la somme \(X_n+Y_n\) converge en loi vers \(X+c\) et que le produit \(X_nY_n\) converge en loi vers \(cX\).
- L’hypothèse dans le théorème selon laquelle \(Y_n\) converge en probabilité vers une constante \(c\) est équivalente à l’hypothèse \(Y_n\) converge en loi vers une constante \(c\).
- Le théorème ne s’applique plus si les deux suites de variables aléatoires tendent toutes deux vers une variable aléatoire et non une constante.
- Le théorème reste cependant vrai si les deux variables tendent toutes deux vers deux constantes distinctes.
- Rappel : on dit que la suite de variables aléatoires \((Y_n)_{n\in\mathbb{N}}\) converge en probabilité vers la constante \(c\) et on note \(Y_n\overset{\mathbb{P}}{\rightarrow}c\) si et seulement si : \[\forall \epsilon >0, \lim\limits_{n\to +\infty} P([ |Y_n-c| > \epsilon])=0\]
- Rappel : on dit que la suite de variables aléatoires \((X_n)_{n\in\mathbb{N}}\) converge en loi vers la variable aléatoire \(X\) et on note \(X_n\overset{\mathcal{L}}{\rightarrow}X\) si et seulement si : \[\forall x \in D_X, \lim\limits_{n\to +\infty} F_{X_n}(x)=F_X(x)\] où \(D_X\) désigne l’ensemble des points de continuité de la fonction de répartition de \(X\), c’est-à-dire \(F_X\).
Les sujets de concours avec le théorème de Slutsky
Ce théorème étant au programme pour la filière ECS, on le retrouve dans de nombreux sujets de concours. En voici une liste non exhaustive pour te familiariser avec cette notion :