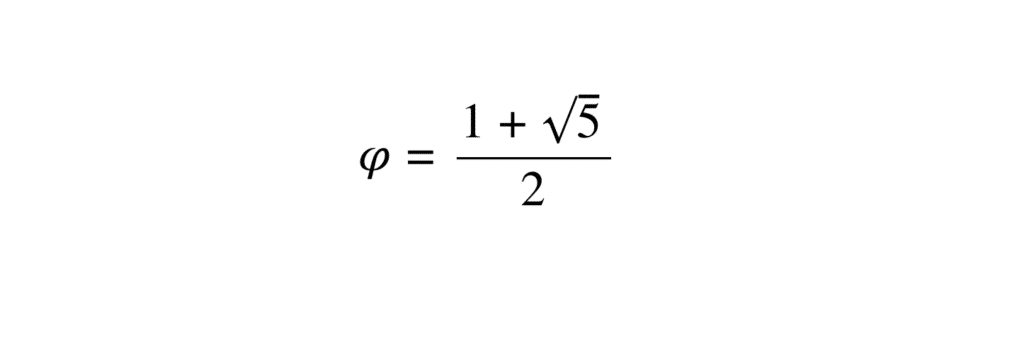Le nombre d’or, souvent noté par la lettre grecque \(\varphi\) (phi), est un nombre irrationnel qui a fasciné les mathématiciens (notamment Leonardo Fibonacci), les artistes et les architectes depuis des siècles. Le nombre d’or est souvent associé à des proportions esthétiquement plaisantes et apparaît dans divers domaines, de la nature à l’art en passant par les finances. Dans cet article, nous explorerons les propriétés mathématiques du nombre d’or, ses apparitions dans différents contextes et quelques applications pratiques. Le nombre d’or est une notion hors programme ECG qui est très en vogue ces derniers temps et pourrait faire l’objet, avec la suite de Fibonacci, d’un sujet de maths aussi bien de province que de parisiennes…
Définition du nombre d’or
Le nombre d’or, souvent noté par la lettre grecque \(\varphi\) (phi), est un nombre irrationnel avec des propriétés fascinantes. Il peut être défini de plusieurs manières.
Il est défini comme le nombre suivant :
\[ \varphi = \frac{1 + \sqrt{5}}{2} \approx 1,618 \]
Il peut également être défini par la relation :
\[ \varphi = 1 + \frac{1}{\varphi} \]
Cette dernière équation peut être réécrite sous la forme d’une équation quadratique :
\[ \varphi^2 – \varphi – 1 = 0 \]
Résolvons cette équation quadratique pour vérifier notre définition :
\[ \varphi = \frac{1 \pm \sqrt{1 + 4}}{2} = \frac{1 \pm \sqrt{5}}{2} \]
Comme nous cherchons le nombre positif, nous obtenons :
\[ \varphi = \frac{1 + \sqrt{5}}{2} \]
Ainsi, le nombre d’or peut être défini comme le nombre positif qui, lorsqu’on lui ajoute 1, est égal à son carré.
Une autre manière courante de définir le nombre d’or est par le rapport de deux segments de ligne. Considérons un segment de ligne divisé en deux parties, \( a \) et \( b \), où \( a \) est la partie plus longue et \( b \) est la partie plus courte. Le rapport entre la longueur totale \( (a + b) \) et la longueur de la partie plus longue \( a \) est égal au rapport entre la longueur de la partie plus longue \( a \) et la longueur de la partie plus courte \( b \). Mathématiquement, cela se traduit par :
\[ \frac{a + b}{a} = \frac{a}{b} = \varphi \]
Ces différentes représentations et décompositions illustrent la complexité et la richesse mathématique du nombre d’or, ainsi que sa présence dans diverses structures et formes.
À lire également : le problème des lapins de Fibonacci, une merveilleuse illustration du nombre d’or dans la nature.
Propriétés algébriques du nombre d’or
Le nombre d’or possède plusieurs propriétés intéressantes. Voici deux de ses propriétés les plus remarquables : l’autosimilarité et son lien avec la suite de Fibonacci.
Autosimilarité
Le nombre d’or est unique en ce sens que son carré et son inverse respectent des identités intéressantes :
\[ \varphi^2 = \varphi + 1 \]
\[ \frac{1}{\varphi} = \varphi – 1 \]
Carré du nombre d’or
Partons de la définition du nombre d’or :
\[ \varphi = 1 + \frac{1}{\varphi} \]
Multiplions les deux côtés de cette équation par \(\varphi\) :
\[ \varphi^2 = \varphi \cdot 1 + \varphi \cdot \frac{1}{\varphi} \]
Ainsi, nous obtenons :
\[ \varphi^2 = \varphi + 1 \]
Suite de Fibonacci et ses liens avec le nombre d’or
Les rapports entre les termes successifs de la suite de Fibonacci convergent vers le nombre d’or. Si \( F_n \) représente le \( n \)-ième terme de la suite de Fibonacci, alors :
\[ \lim_{n \to \infty} \frac{F_{n+1}}{F_n} = \phi \]
En effet, la suite de Fibonacci est définie par la relation de récurrence suivante :
\[ F_{n+2} = F_{n+1} + F_n \]
(Cette récurrence constitue également l’un des fondements des matrices de Fibonacci.)
Considérons le rapport de deux termes consécutifs de la suite :
\[ \frac{F_{n+2}}{F_{n+1}} = \frac{F_{n+1} + F_n}{F_{n+1}} = 1 + \frac{F_n}{F_{n+1}} \]
Posons \( \frac{F_{n+1}}{F_n} = r_n \). Alors, nous avons :
\[ r_{n+1} = 1 + \frac{1}{r_n} \]
Lorsque \( n \) tend vers l’infini, \( r_n \) converge vers un nombre limite \( L \). Donc :
\[ L = 1 + \frac{1}{L} \]
En multipliant les deux côtés de l’équation par \( L \), nous obtenons :
\[ L^2 = L + 1 \]
Cette équation est identique à l’équation quadratique définissant le nombre d’or, donc \( L = \varphi \).
Ainsi, nous avons montré que les rapports entre les termes successifs de la suite de Fibonacci convergent vers le nombre d’or.
Propriétés algébriques avancées du nombre d’or
Comme nous l’avons vu, le nombre d’or, noté \( \varphi,\) vérifie la relation \( \varphi^2=\varphi+1,\) ce qui signifie également que \(\displaystyle \varphi-1= \frac{1}{\varphi}.\)
Ces propriétés permettent d’écrire le nombre d’or sous différentes formes intéressantes, notamment sous forme de racines carrées imbriquées et de séries géométriques.
Racines carrées imbriquées
Le nombre d’or peut être exprimé sous forme de racines carrées imbriquées de la manière suivante :
\[ \varphi = \sqrt{1 + \varphi} = \sqrt{1 + \sqrt{1 + \varphi}} = \sqrt{1 + \sqrt{1 + \sqrt{1 + \sqrt{1 + \cdots}}}} \]
Cette représentation montre l’autosimilarité du nombre d’or et la manière dont il peut être construit à partir d’itérations infinies de racines carrées. Pour démontrer cette propriété, commençons par sa définition :
\[ \varphi = 1 + \frac{1}{\varphi} \]
Multiplions chaque côté par \(\varphi\) pour obtenir :
\[ \varphi^2 = \varphi + 1 \]
Prenons maintenant la racine carrée des deux côtés :
\[ \varphi = \sqrt{1+\varphi} \]
Remplaçons à nouveau \(\varphi\) par \(\sqrt{1 + \varphi}\) :
\[ \varphi = \sqrt{1 + \sqrt{1 + \varphi}} \]
En répétant ce processus indéfiniment, nous obtenons :
\[ \varphi = \sqrt{1 + \sqrt{1 + \sqrt{1 + \sqrt{1 + \cdots}}}} \]
Ainsi, nous avons démontré que le nombre d’or peut être représenté comme une racine carrée imbriquée infinie.
Séries géométriques et nombre d’or
Le nombre d’or peut également être exprimé sous forme de séries géométriques :
\[ \varphi = \sum_{k=1}^{\infty} \frac{1}{\varphi^k} \; \text{et} \; \varphi = \sum_{k=0}^{\infty} \frac{1}{\varphi^{2k}} \]
Ces séries montrent comment il peut être décomposé en une somme infinie de fractions. La première série utilise la décomposition en termes de puissances décroissantes de \(\varphi,\) tandis que la deuxième utilise les puissances paires de \(\varphi.\)
Ces différentes représentations et décompositions illustrent la complexité et la richesse mathématique du nombre d’or, ainsi que sa présence dans diverses structures et formes.
Le nombre d’or dans la nature et l’art
Le nombre d’or apparaît fréquemment dans la nature, par exemple dans les spirales des coquillages, les arrangements des feuilles autour des tiges, et les proportions du corps humain. En art et en architecture, il est utilisé pour créer des compositions équilibrées et esthétiquement plaisantes.
Exemples du nombre d’or dans la nature
1. Spirales : les spirales logarithmiques, comme celles observées dans les coquillages et les galaxies, suivent souvent une croissance proportionnelle au nombre d’or.
2. Phyllotaxie : l’arrangement des feuilles autour d’une tige, appelé phyllotaxie, tend à suivre un motif où les angles successifs sont approximativement des fractions du nombre d’or, optimisant ainsi l’exposition à la lumière et à l’air.
Exemples du nombre d’or dans l’art et l’architecture
1. Parthénon : les proportions du Parthénon en Grèce antique sont souvent associées au nombre d’or.
2. Peinture et sculpture : de nombreux artistes de la Renaissance, comme Léonard de Vinci, ont utilisé le nombre d’or pour créer des œuvres équilibrées et harmonieuses.
Le rectangle d’or
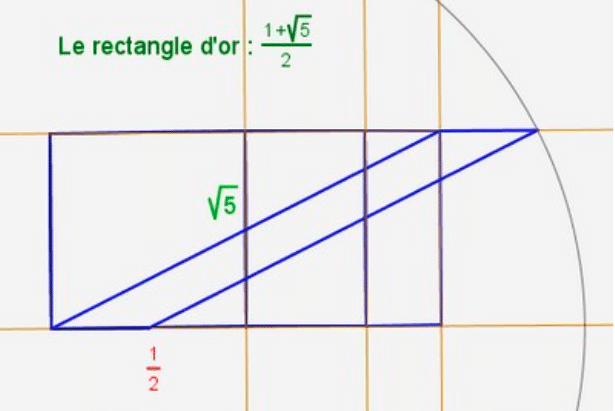
Le rectangle d’or est une figure géométrique caractérisée par un rapport entre sa longueur \( L \) et sa largeur \( W \) égal au nombre d’or \( \varphi = \frac{1 + \sqrt{5}}{2} \). Ce rapport confère au rectangle une propriété d’autosimilarité. Si l’on soustrait un carré de côté \( W \) de ce rectangle, la figure restante est elle-même un rectangle d’or. Mathématiquement, pour un rectangle d’or, on a :
\[
\frac{L}{W} = \varphi
\]
et après avoir enlevé un carré, le nouveau rectangle conserve ce rapport. Cette propriété, transposable avec le nombre d’argent, donne le rectangle d’or. Elles montrent comment les nombres d’or et d’argent se manifestent naturellement dans certaines constructions géométriques.
Aller plus loin sur le nombre d’or
Le nombre d’or est à l’origine de nombreuses recherches et nombreux problèmes mathématiques. Pour y voir plus clair, voici une cartographie de l’ensemble des recherches tournant autour (et de la suite de Fibonacci) :
| Tableau de correspondances suites/nombres (en lien avec Fibonacci/nombres métalliques) | |
| Suites | Nombres |
| Suite de Fibonacci | Nombre d’or |
| Suite de Pell | Nombre d’argent |
| Généralisation de Fibonacci : les suites k-bonacci | Nombres métalliques : généralisation du nombre d’or |
| Suite de Lucas | Nombre de Lucas |
| Suite de Padovan | Nombre plastique |
| Suite de Perrin | Nombres pseudo-premiers de Perrin |
| Suite de Jacobsthal | Nombres oblongs de Jacobsthal |
| Polynôme/suite de Narayana | Nombre de Narayana |
| Nombre de Gildas | |
| Nombre de Keith | |
| Super nombre d’or | |
Un autre type de généralisation de la suite de Fibonacci et donc du nombre d’or dérivé sous diverses formes est également à découvrir ! Il s’agit de la suite de Fibonacci aléatoire. Elle pourrait clairement faire l’objet d’un sujet de maths parisienne dans les années à venir…
A lire également : le triangle de Pascal (et ses liens avec la suite de Fibonacci/le nombre d’or) & les liens entre nombre d’or et pi
Conclusion sur le nombre d’or
Le nombre d’or est une constante mathématique fascinante qui joue un rôle important dans divers domaines, de la nature à l’art en passant par l’architecture. Sa propriété unique de s’autorépliquer à travers différentes échelles et ses apparitions récurrentes dans des contextes esthétiques en font un sujet d’étude captivant et utile pour les épreuves écrites et orales de mathématiques.
Ainsi, bien qu’il soit hors programme, la compréhension approfondie des propriétés liées à ce nombre te permettra d’améliorer tes compétences en analyse, te préparant donc pour les épreuves écrites et orales. Pour t’entraîner sur cette notion, tu peux réaliser les sujets suivants :
- Ecricome 2018 (mathématiques approfondies),
- Maths 1 HEC 2009 (mathématiques appliquées),
- la première Question Sans Préparation des Oraux HEC 2023.
Tu peux retrouver le méga-répertoire qui contient toutes les annales de concours et les corrigés. Tu peux également accéder à toutes nos autres ressources mathématiques.