Dans les exercices de concours, il arrive fréquemment qu’il soit demandé de représenter graphiquement une fonction. Or, même si ce genre de questions présente un bon rapport point/temps, beaucoup de candidats les délaissent, faute de savoir les traiter correctement.
Dans cet article, tu retrouveras donc les différentes étapes à suivre pour tracer parfaitement le graphe d’une quelconque fonction \(f\).
Étude des dérivées première et seconde de \(f\)
Avant toute chose, il est nécessaire de déterminer le domaine de définition de \(f\). Une fois ceci fait, il s’agit d’étudier l’existence des dérivées première et seconde de \(f\). De fait, tu devras successivement t’intéresser à la dérivabilité de \(f\), puis de \(f’\).
En général, la fonction étudiée est la composition de plusieurs fonctions usuelles. Donc, il s’agira de revenir sur ce que tu sais concernant ces dernières.
Ainsi, détermine \(f’\) et \(f^{(2)}\), puis sers-t’en pour faire un tableau de variations. D’abord, avec le signe de \(f’\), tu pourras déterminer les variations de \(f\) ainsi que ses points critiques. Ensuite, avec le signe de \(f^{(2)}\), tu pourras déterminer les intervalles sur lesquels \(f\) est convexe ou concave. Par là même, tu pourras déterminer les points d’inflexion de \(f\). C’est-à-dire les points en lesquels \(f\) passe de convexe à concave ou inversement.
Petit rappel : si \(f^{(2)}\) est de signe positif (resp. négatif) sur un intervalle \(I\), alors \(f\) est convexe (resp. concave) sur \(I\).
Avant de représenter la courbe
Ensuite, choisis un intervalle sur lequel tu vas pouvoir tracer ta courbe. En général, il s’agira de prendre un intervalle classique, du genre \([-5,5]\), \([-1,1]\) ou autre. Ce qui importe, c’est que l’intervalle choisi soit le plus représentatif possible du comportement de \(f\).
Ensuite, il s’agira de déterminer les équations des tangentes de \(f\) en ses points d’inflexion, que tu as pu déterminer précédemment.
Représenter \(f\)
Une fois tout ceci fait, il est temps de tracer la courbe de \(f\). Commence par tracer les tangentes que tu as déterminées. Par la suite, sers-t’en pour déterminer approximativement l’allure de la courbe. Enfin, essaie d’aiguiller le traçage de ta courbe en prenant pour repères les valeurs prises par \(f\) en certains points de l’intervalle considéré.
Pour plus de concret, nous allons prendre un exemple.
Un exemple de représentation graphique
Nous prendrons ainsi comme exemple la fonction \(f\) définie par :
\( \forall x \in \mathbb{R}, f(x)= \exp(-\exp(-x)) \)
D’abord, \(f\) est bien définie sur \( \mathbb{R} \) comme composée de fonctions qui le sont. De plus, pour les mêmes raisons, elle est de classe \( C^2 \). Déterminons ainsi \(f’\) et \(f^{(2)}\).
\( \forall x \in \mathbb{R}, f'(x)= \exp(-x) \times \exp(-\exp(-x)) \)
On sait que la fonction \( \exp \) est à valeurs strictement positives sur \( \mathbb{R} \). Donc, on a clairement : \( \forall x \in \mathbb{R}, f'(x) \ge 0 \)
Maintenant, on va déterminer \(f^{(2)}\).
\(\forall x \in \mathbb{R}, f^{(2)}(x)\)
\(=-\exp(-x)\times\exp(-\exp(-x))+\exp(-x)\times\exp(-x)\times\exp(-\exp(-x))\)
On a alors :
\( \begin{align} f^{(2)}(x)=0 \\& \Leftrightarrow \exp(-x) \times \exp(-\exp(-x)) \times (-1 + \exp(-x)) = 0 \\& \Leftrightarrow \exp(-x) = 1 \\& \Leftrightarrow x = 0 \end{align} \)
Donc, le seul point d’inflexion de \(f\) est le point d’abscisse x=0.
Ainsi, d’après les résultats précédents, on obtient le tableau de variation suivant :
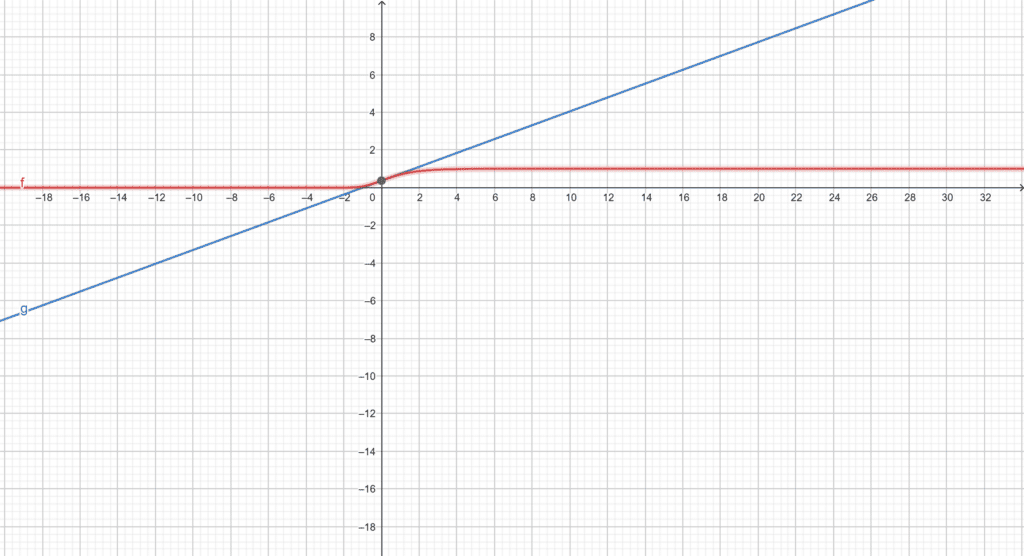
On peut donc désormais tracer le graphe de \(f\). Mais avant cela, on représente la tangente à la courbe de \(f\) au point d’abscisse 0. C’est-à-dire en l’unique point d’inflexion de \(f\).
Ensuite, on représente \(f\) grâce aux informations précédemment obtenues.
J’espère que cet article t’aura été utile. Tu peux retrouver toutes nos ressources en maths juste ici !